Circuitos combinacionais

Ao combinar as portas lógicas que vimos até aqui, podemos criar muitos tipos diferentes de circuitos que nos ajudam a resolver muitos problemas. Esses circuitos tem a seguinte característica: a sua saída, em um determinado momento, depende apenas das entradas nesse mesmo momento. Ou seja, eles não dependem de entradas/saídas que foram obtidas no passado, nem de algum tipo de memória. Tais circuitos são conhecidos como circuitos combinacionais, devido à sua saída depender apenas das combinações das entradas em um determinado instante.

Veremos nesse capítulo como criar circuitos combinacionais que resolvam algum problema real.

Projetando Circuitos Lógicos Combinacionais

Existem diversas técninas para projetar um circuito combinacional para resolver um problema específico, algumas técnicas são simples e podemos fazer manualmente, algumas outras são feitas com a ajuda de programas de computador. Algumas possuem princípios básicos necessários para fazer a análise e criação do circuito.

Um dos principíos básicos, é a criação de uma tabela verdade que descreva o resultado do nosso circuito, com isso podemos pensar combinações de portas lógicas que satisfaçam essa tabela.

Além disso, existe um padrão de circuitos que eventualmente aparece enquanto estamos projetando o nosso circuito, esse padrão é conhecido como “Soma-de-Produtos”, veremos esse padrão a seguir, e depois, veremos como projetar um circuito que esteja utilizando esse padrão.

Soma-de-Produtos

Um circuito está na forma de soma-de-produtos quando todas as entradas do circuito estão conectadas a portas AND e a saída dessas portas são entradas para uma porta OR, que por sua vez pode ter diversas entradas, dependendo apenas da quantidade de portas AND que estarão conectadas. Além disso, as entradas do circuito podem ou não estar conectadas a um inversor. Veja um exemplo de circuito que está no formato soma-de-produtos:

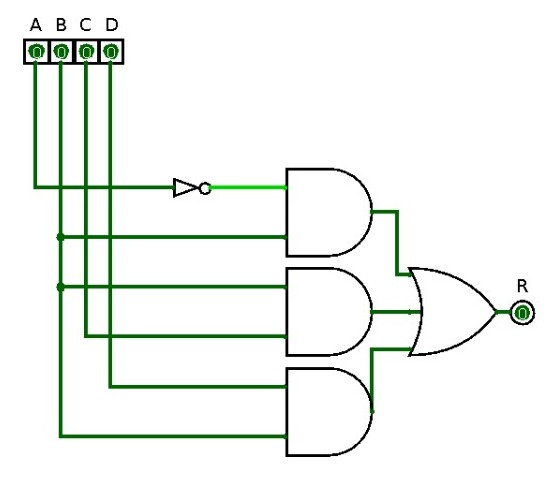
Neste circuito, perceba que todas as entradas então conectadas ao AND e todas as saídas dos AND estão conectados ao OR, e que também é possivel que uma entrada esteja invertida, como é o caso da entrada A. Veja como seria a representação algébrica desse circuito:

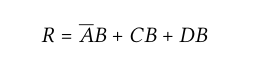
Nesse caso,R representa a saída do circuito. Perceba que a representação algébrica do circuito é uma soma de produtos, por esse motivo que esse formato possue o nome de soma-de-produtos

Exemplo de circuito utilizando a soma de produtos

Agora com as ideias básicas, veremos como criar um circuito para resolver problemas. Iremos descrever um problema e resolve-lo para que o leitor entenda os passos básicos para a resolução de qualquer problema semelhante.

Descrição do problema:

Queremos implementar um circuito onde a sua saída esteja ativa quando ao menos duas das suas três entradas estiverem ativas.

Dado o problema, o primeiro passo é descrever uma tabela verdade que represente o comportamento que queremos. A tabela é descrita da seguinte forma:

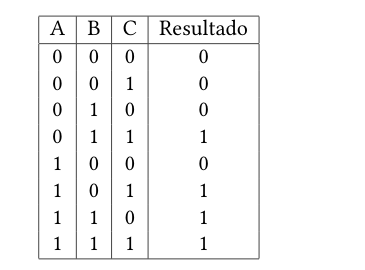
Agora precisamos verificar cada linha que tenha a saída ativa, e montar uma expressao AND com as entradas daquela linha. Veja como montar essa expressão para cada linha da tabela verdade:

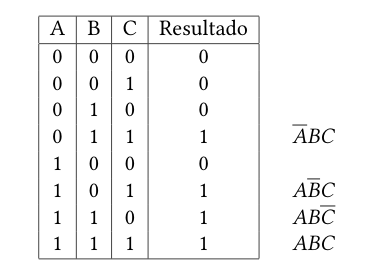
No circuito, essas expressão são construídas conectando todas as entradas da sua respectiva linha a uma porta AND. Quando alguma entrada naquela linha estiver em zero (0), é necessário primeiro conecta-las a um inversor (porta NOT) antes de serem conectadas na porta AND, fazendo com que a saída do inversor fique ativa.

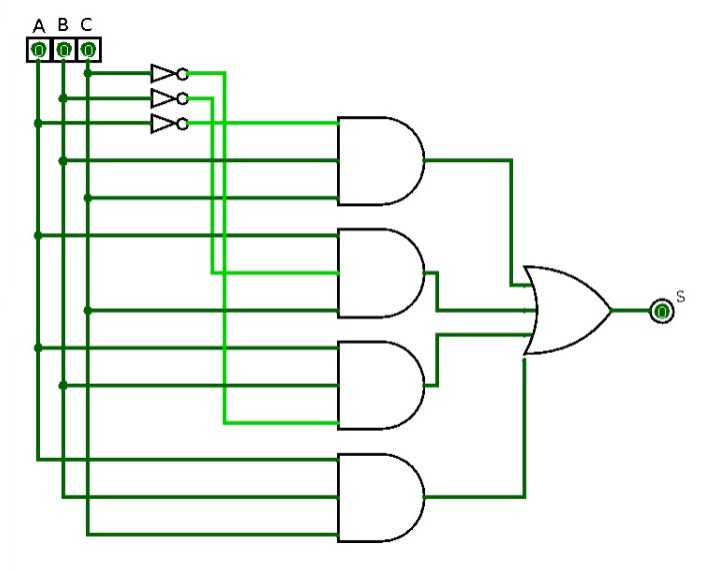
Após isso, todas as saídas das expressões AND serão conectadas a uma porta OR, formando um circuito de soma-de-produtos, finalizando assim, o circuito. Veja a representação final na forma de expressão algébrica e na forma de circuito:

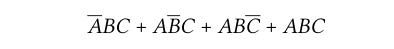
Posts Seguintes

Com essa ideia, podemos criar uma variadade de circuitos, no final desses posts será utilizado essa ideia para fazer uma automação em minecraft. Pórem, antes de iniciarmos, iremos ver outros dispositivos e técnicas que irão complementar nosso conhecimento necessário para execução do projeto.

• O próximos post é: Dispositivos com memória
• O post anterior a este é: Portas NAND e NOR
• Seção com todos os artigos: sumário